3.1 Preliminaries
Before introducing our framework, we first present MCTS to clarify the motivation behind our work.
MCTS Coulom (2006) is a widely used planning algorithm and famously employed in AlphaGo Silver et al. (2016).
Taking the Game of Go as an example, the algorithm assists in selecting the best possible action in the current state of the board based on their average rewards.
These rewards are obtained through numerous simulations.
For instance, consider the current state where action a1 is chosen as the next move.
The game then proceeds to completion, with all subsequent actions, whether by our side or the opponent, determined by a policy model rather than a real player.
The entire game sequence constitutes one simulation of action a1.
If we win, the reward is 1; otherwise, it is 0.
Specifically, if we simulate 10 games from the current state with action a1 and win 9 of them, the average reward for a1 would be 0.9.
However, due to the vast action space in the Game of Go, it is impractical to simulate every possible action.
The Upper Confidence Bound 1 applied to Trees (UCT) identifies actions with higher potential to win, allocating more simulations to these actions rather than distributing simulations equally among all actions.
Once an action is decided based on this process and physically executed, leading to a new game state, the same procedure is then applied to select actions from this new state, and the planning continues until the actual end of the Game of Go.
MCTS typically involves four key procedures:
Selection: Traverse the current reasoning tree to select the node with the highest UCT for simulation.
Expansion: Extend the reasoning tree by adding new child nodes from the selected node.
Simulation: Continue expanding from these child nodes until a simulation is completed.
Backpropagation: After each simulation, update the average reward of corresponding nodes with the newly obtained simulation reward.
3.2 Framework of MASTER
In our framework, MASTER, the concepts of reasoning tree, selection, expansion, and backpropagation are analogous to those used in MCTS.
However, we eliminate the simulation step due to those two issues highlighted in the Introduction section.
Instead, our framework incorporates three special mechanisms to derive rewards: providing more context before self-evaluation, incorporating LLM’s confidence in our novel UCT formula, and updating rewards in backpropagation.
The details of our framework are demonstrated in Figure 1 and further explained in following paragraphs.
When our framework is presented with a problem, it initializes a root agent with the problem.
This agent then prompts the LLM to produce a verbal thought reflecting on the current reasoning trace (Thought) and to propose an action to solve the problem (Action).
The agent subsequently executes this action by tools that interact with the external environment, providing feedback (Observation).
The texts produced, including Thought, Action, and Observation, form the Solution of the agent, as shown in Figure 1.
Next, the agent invokes the LLM to generate a textual output that validates the key facts in the current Solution (Validation).
Finally, the agent prompts the LLM to assess the progress made towards solving the problem, producing a score and the LLM’s confidence to this score in the response (Assessment).
These two values (score and confidence) are then extracted. All texts (Solution, Validation, Assessment) constitute the Context of the agent and are stored in its memory (Figure 1). The score serves as the initial reward for this agent.
The previous paragraph describes the generation of a single agent in our system.
After the root agent is generated, child agents are created following the same procedure, with the root agent’s Context appended to the prompts of these child agents, as they need to continue solving the problem.
As illustrated in Figure 1, two child agents (Agent1 and Agent2) are generated using exactly the same procedure and prompt to explore diverse reasoning paths from the same state (parent agent).
The number of child agents is a hyperparameter, Number of Branches, which varies depending on the task.
The creation of these child agents is termed expansion from the parent agent.
Further expansion can be carried out from any existing agent using the same procedure.
The UCT of each agent is calculated, and the agent with the highest UCT is selected for further expansion.
Another hyperparameter, Maximum of Expansion, represents the approximate number of steps required to solve the problem, allowing users to set it based on their understanding of the task.
If this limit is reached without finding a satisfactory solution, the solution from the terminal agent with the highest reward is submitted as the final answer.
During the expansion of the reasoning tree, agents that generate a final answer rather than an intermediate step in their Solution are called Terminal Agents.
For instance, in the HotpotQA task, if an agent’s Action is ’Finish[]’, it is identified as a terminal agent, as this Action indicates a final answer.
Similar indicators exist in the Solution of other tasks.
During the Evaluation (Figure 1), the LLM assesses the correctness of the Solution.
If the LLM deems the solution correct, it is submitted as the final answer, concluding the task.
If not, backpropagation is triggered, using the reward from this terminal agent to update the rewards of all agents on the path up to the root agent. Pseudo code can be found in Appendix A.
3.3 Formula of Modified UCT
Recent works RAP and LATS directly apply the original UCT formula. To better suit our design, we propose a modified UCT formula.
The original UCT formula is derived from Hoeffding’s Inequality Lattimore T (2020) which can be found in Appendix B.
It is typically applied in the following scenario: Given a node representing a state (referred to as nodeh), there are multiple subsequent actions to choose from (e.g., a_i,a_j,a_k).
To determine the Q value of these actions, multiple simulations are conducted, and UCT is employed to decide which action should be simulated.
Instead of simply selecting the node with the highest Q value (pure exploitation, the first term in Eqn 1), UCT balances exploitation and exploration by incorporating an exploration term (the second term in Eqn 1) that favors nodes with fewer simulations.
The node_i, representing the state resulting from action a_i, is one of the child nodes of node_h. The UCT formula for nodei is:

Where n_i is the number of backpropagations applied to the node_i. r_n is the reward of the n-th backpropagation.
Q_i is the estimation of Q value calculated by Eqn 2.
It represents the average reward from simulations.
N_i is the total number of simulations by the parent node of the current nodei which is node_h.
In other words, N_i is the sum of n_i, n_j and n_k in above example although n_j and n_k are not explicitly shown in the UCT formula.
In our system, Q_i, as the estimation of Q value, consists of two components: Initial Reward is extracted from Assessment when this agent is generated.
Updating Reward is the mean of rewards from backpropagation, similar to Q_i in Eqn 2. Inspired by the research on auxiliary information about rewards in the form of control variables Verma and Hanawal (2021), we modify the reward estimation in our system as shown in Eqn 3:
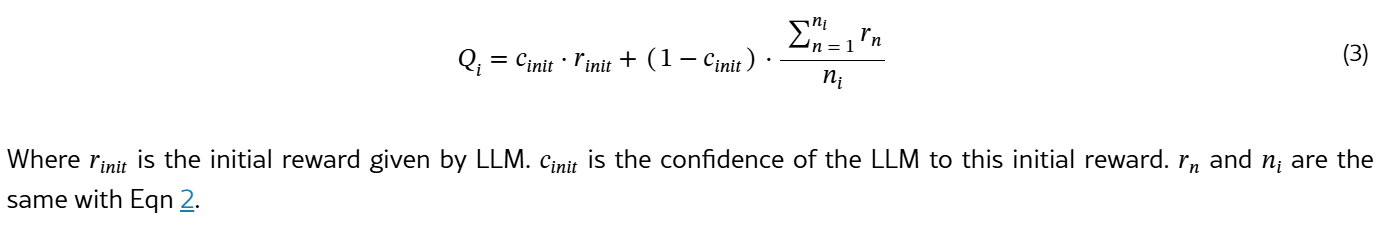
Where r_init is the initial reward given by LLM. c_init is the confidence of the LLM to this initial reward. r_n and n_i are the same with Eqn 2.
The original MCTS relies heavily on numerous simulations to make this estimation accurate.
Hence it is not reliable if the number of n_i is small.
On the other hand, our Q value has an extra component (initial reward), as our Q value is the weighted sum of initial reward and updating reward with the confidence as weight.
When LLM has high confidence to the initial reward it assigns, fewer backpropagations are needed and the influence of rewards from backpropagation (updating reward) is reduced due to its lower weight.
Conversely, when the LLM has low confidence, more backpropagations are required to dominate the Q value estimation, so the exploration term according to this cinit as introduced in next paragraph is increased and the weight of updating reward (1−c_init) is higher.
In the formula used by RAP and LATS, there is an exploration constant c instead of the fixed 1/ sqrt(2) as the weight of the exploration term as following:

In our approach, we use 1/(10 x 루트2 x c_init) as the exploration weight.
The significance of this adjustment is twofold: 1).
The exploration term reflects the uncertainty associated with this agent.
When the LLM has low confidence in the initial reward, the agent’s uncertainty is relatively high, necessitating more exploration.
In such cases, a higher exploration weight increases the UCT, guiding the algorithm to select this agent for further exploration.
2).The number of backpropagations in our system is significantly lower than in the original MCTS while the slope of the logarithmic function is relatively steep when the variable is small, so the value of the exploration term tends to play a dominant role.
Therefore, this exploration weight should be used to control the influence of this term.
Moreover, when the minimum confidence of 0.1 is used, the exploration weight equals 1/ sqrt(2), the same as the weight in Eqn 1.
In summary, the revised formula in our system is:
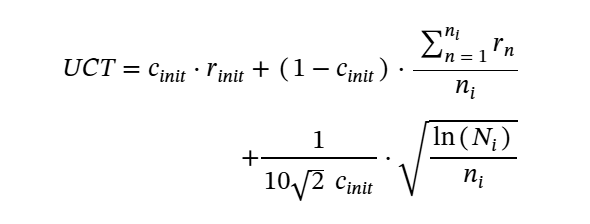
3.4 Strategies of Reward Assignment
To conclude, the three special mechanisms we implement to ensure the reliability of rewards in our framework are:
1). Before assigning a reward in the Assessment phase, an additional Validation step is conducted, where the LLM comments on the correctness of the facts in the current solution.
These comments are added to the prompt for the Assessment step, guiding the LLM toward a more reliable reward.
This design is motivated by the observation that the LLM performs better when it is asked to address one problem at a time. Separately verifying correctness and progress can lead to stable and reliable scoring.
2). In the Assessment phase, the LLM is asked to provide both a score and its confidence in that score, rather than just the score alone.
The confidence value plays two roles in our modified UCT formula, which is detailed in the Formula of Modified UCT subsection.
If the LLM has low confidence in the score it provides, the influence of this score is reduced and the likelihood to select this agent for further exploration is increased.
3). Backpropagation occurs after each simulation in the original MCTS.
Although we have removed simulations, backpropagation is retained in our framework.
It is triggered whenever a terminal agent produces a Solution that fails Evaluation.
A failed Evaluation indicates that the reasoning steps leading to this terminal agent may be flawed, and their Q value should be reduced accordingly.
This mechanism allows for the adjustment of rewards if they are inaccurate at the outset.