Scaling LLM Test-Time Compute Optimally canbe More Effective than Scaling Model Parameters 논문리뷰

https://arxiv.org/abs/2408.03314

(1) searching against dense, process-based verifier reward models; and

(2) updating the model’s distribution over a response adaptively, given the prompt at test time. We find that in both cases, the effectiveness of different approaches to scaling test-time compute critically varies depending on the difficulty of the prompt

모델 크기를 키우는 것과 test-time에 추가 계산을 수행하는 것 중 어느 것이 더 효과적인지를 다양한 상황에서 비교 분석

 

For example, on easier problems, for which the base LLM can already readily produce reasonable responses, allowing the model to iteratively refine its initial answer by predicting a sequence of N revisions (i.e., modifying the proposal distribution), may be a more effective use of test-time compute than sampling N independent responses in parallel.

쉬운문제의 경우 LLM이 상당한 response들을 readily하게 생성할수 있으므로 N개의 revision sequence를 예측함으로써 첫 답변을 refine하는게 병렬로 N개의 독립적인 답변을 샘플링 하는것보다 효율적일 수 있다

 

On the other hand, with more difficult problems that may require searching over many different high-level approaches to solving the problem, re-sampling new responses independently in parallel or deploying tree-search against a process-based reward model is likely a more effective way to use test-time computation

해결하기 위해 high-level approach를 search하는것이 필요할지모르는 어려운 문제는 

새로운 답변들을 병렬로 independently하게 re-sampling하거나 또는 tree-search와 같은 approach가 효율적일 수 있다

 

-> This finding illustrates the need to deploy an adaptive “compute-optimal“ strategy for scaling test-time compute

wherein the specific approach for utilizing test-time compute is selected depending on the prompt, so as to make the best use of additional computation

프롬프트에 따라 test-compute를 선택하고 추가계산을 best하게 활용

사람들은 더 좋은 의사결정을 위해 오래 사고하는 경향이 있다

이와 비슷한 능력을 LLM에서 instill할 수 없을까?

기존의 test-time computation을 이용해

self-refine, enhanced factuality via multi debate, Tree of thoughts

결과물을 형상시키는 연구

 

그와 반대로 이러한 효과의 효율성이 remain limited라는 연구또한 LLM cannot self correct reasoning yet, Gpt-4 doesn’t know it’s wrong과 같은 존재

 

So

->> motivate the need for a systematic analysis of different approaches for scaling test-time compute.

가장 간단하고 well-studied 된 approach는 Best of N으로

2. A Unified Perspective on Test-Time Computation: Proposer and Verifier

 

(1) at the input level

 

(2) at the output level

(2-1)naïvely conditioning on the prompt

(2-2)verifiers ,scorers 

-> proposal distribution 를 modify

위의 두 과정은 Markov chain Monte Carlo (MCMC) sampling from a complex target distribution과 유사

하지만 combining a simple proposal distribution and a score function라는 점이 다름

또한 self-critique과 같은 방식도 존재

 

그외에도 we utilize the approach of finetuning on on-policy data with Best-of-N guided improvements to the model response == recursive introspection

https://arxiv.org/pdf/2407.18219v1

 

또다른 방법에는 STaR, ReST 와 같은 RL-inspired finetuning methods 가 있다

추가적인 input 토큰 사용 없이 향상된 proposal distribution로 induce, 유도하도록 모델을 fine tune하는 방법

 

3. How to Scale Test-Time Computation Optimally

 

revision을 위해 미세조정된 model과 verifier로써 ORM을 사용할떄,

we could either spend the full test-time compute budget on generating N independent samples in parallel from the model and then apply best-of-N,

N개의 독립적인 샘플들을 병렬로 생성하기 위해 full test-time compute budget을 사용후 best-of-N을 적용하거나

or we could sample N revisions in sequence using a revision model and then select the best answer in the sequence with an ORM

N개의 revision 샘플을 revision model을 사용해 생성후 ORM으로 best 답변을 선택하거나

or strike a balance between these extremes

위의 두 양극 사이의 밸런스를 조절할수도 잇다

 

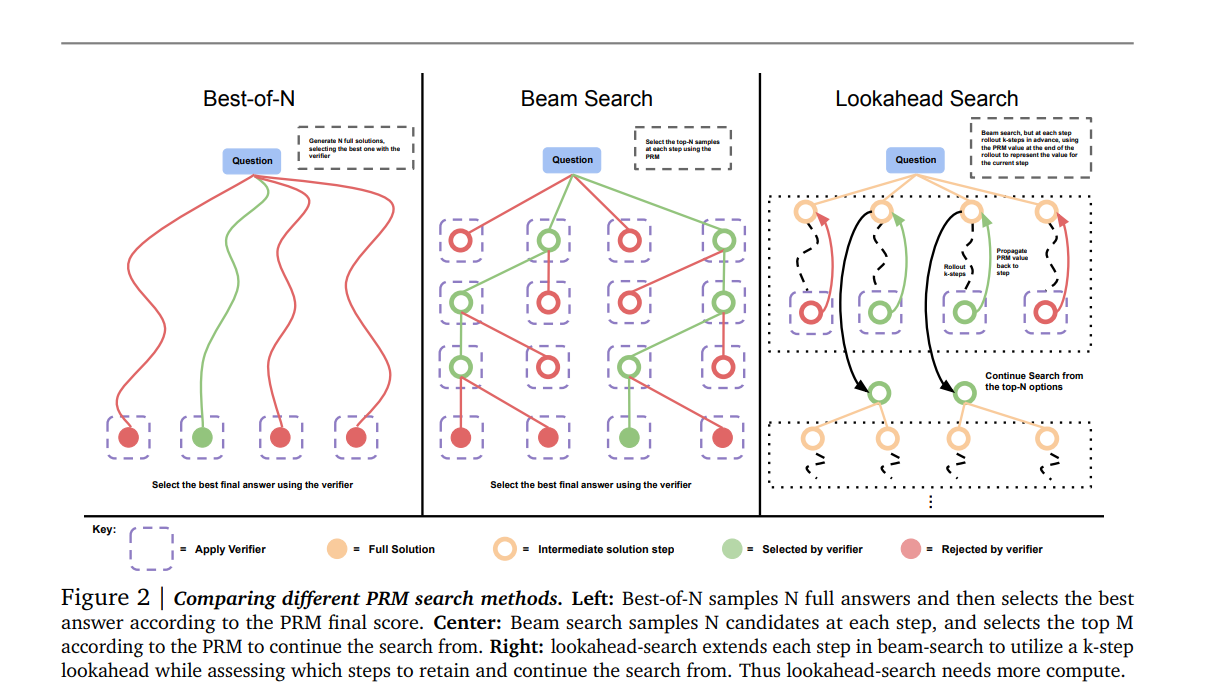
In the case of verifiers, 여러 search algorithms 옵션이 존재한다(e.g. beam-search, lookahead-search, best-of-N)

이는 어려운 문제에서 simpler best-of-N 또는 majority baseline 효과적일수잇다

 

3.1. Test-Time Compute-Optimal Scaling Strategy

 

3.2. Estimating Question Difficulty for Compute-Optimal Scaling

질문의 난이도 측정 (compute-optimal scaling을 위한)

비록 이는 approximation solution 즉 추정에 불과함에도 inference-time compute in an ad-hoc or uniformly-sampled manner보다 상당한 향상을 이끌어낸다는것을 발견

 

• Defining difficulty of a problem.
  문제 난이도의 정의이다.
• Following the approach of Lightman et al. [22], we define question difficulty as a function of a given base LLM.
  Lightman 외 [22]의 접근 방식을 따라, 우리는 주어진 기본 LLM의 함수로서 문제의 난이도를 정의한다.
• Specifically, we bin the model’s pass@1 rate – estimated from 2048 samples – on each question in the test set into five quantiles, each corresponding to increasing difficulty levels.
  구체적으로, 우리는 테스트 세트의 각 질문에 대해 2048개의 샘플에서 추정된 모델의 pass@1 비율을 다섯 개의 quantile로 나누며, 각 quantile는 증가하는 난이도 level에 해당한다.
• We found this notion of model-specific difficulty bins to be more predictive of the efficacy of using test-time compute in contrast to the hand-labeled difficulty bins in the MATH dataset.
   MATH 데이터세트에서 수동으로 라벨링된 난이도 구간과 비교했을 때, 이 모델 특유의 난이도 구간 개념이 테스트 시간의 컴퓨팅 사용 효과를 더 잘 예측한다는 것을 발견했다.
• That said, we do note that assessing a question’s difficulty as described above assumes oracle access to a ground-truth correctness checking function, which is of course not available upon deployment where we are only given access to test prompts that we don’t know the answer to.
  그러나, 위에서 설명한 대로 문제의 난이도를 평가하는 것은 실제 정답을 확인할 수 있는 함수에 접근할 수 있다고 가정하지만, 실제로는 우리가 정답을 알 수 없는 테스트 프롬프트만 주어지므로 이는 불가능하다.
• In order to be feasible in practice, a compute-optimal scaling strategy conditioned on difficulty needs to first assess difficulty and then utilize the right scaling strategy to solve this problem.
  실제적으로 가능하려면, 난이도에 따른 최적의 컴퓨팅 확장 전략은 먼저 난이도를 평가한 다음, 이 문제를 해결하기 위해 적절한 확장 전략을 활용해야 한다.
• Therefore, we approximate the problem’s difficulty via a model-predicted notion of difficulty, which performs the same binning procedure over the averaged final answer score from a learned verifier (and not groundtruth answer correctness checks) on the same set of 2048 samples per problem.
  따라서 우리는 문제의 난이도를 모델이 예측한 난이도 개념을 통해 근사화하며, 이는 문제당 동일한 2048개 샘플 집합에서 학습된 검증자의 최종 답변 점수를 평균하여 같은 방식으로 구간을 나누는 절차를 수행한다 (실제 정답 여부를 확인하는 것이 아님).
• We refer to this setting as model-predicted difficulty and the setting which relies on the ground-truth correctness as oracle difficulty.
  우리는 이 설정을 모델 예측 난이도라고 하며, 실제 정답에 의존하는 설정을 오라클 난이도라고 부른다.
• While model-predicted difficulty removes the need for need knowing the ground truth label, estimating difficulty in this way still incurs additional computation cost during inference.
  모델 예측 난이도는 실제 정답 레이블을 알 필요를 없애지만, 이러한 방식으로 난이도를 추정하는 것은 여전히 추론 과정에서 추가적인 계산 비용을 발생시킨다.
• That said, this one-time inference cost can be subsumed within the cost for actually running an inference-time strategy (e.g., when using a verifier, one could use the same inference computation for also running search).
  하지만 이 일회성 추론 비용은 실제로 추론 시간 전략을 실행하는 데 드는 비용 내에 포함될 수 있다 (예: verifier를 사용할 때 동일한 추론 계산을 검색에도 사용할 수 있음).
• More generally, this is akin to exploration-exploitation tradeoff in reinforcement learning: in actual deployment conditions, we must balance the compute spent in assessing difficulty vs applying the most compute-optimal approach.
  더 일반적으로, 이는 강화 학습에서의 탐험-이용 간의 균형 문제와 유사하다: 실제 배포 조건에서는 난이도를 평가하는 데 사용되는 컴퓨팅과 가장 계산 효율적인 접근 방식을 적용하는 것을 균형 있게 조절해야 한다.
• This is a crucial avenue for future work (see Section 8) and our experiments do not account for this cost largely for simplicity, since our goal is to present some of the first results of what is in fact possible by effectively allocating test-time compute.
  이는 미래 연구의 중요한 방향이며 (8장을 참조), 우리의 목표는 테스트 시간의 컴퓨팅을 효과적으로 할당함으로써 실제로 가능한 첫 번째 결과를 제시하는 것이므로, 우리는 이 비용을 크게 고려하지 않았다.
•  

5. Scaling Test-Time Compute via Verifiers

 

PRM800k dataset을 사용했는 PALM 2를 사용하다보니 distribution shift 때문인지 (GPT4 generated) 비효율적이엿다

1. We instead apply the approach of Wang et al. [45] to supervise PRMs without human labels, using estimates of per-step correctness obtained from running Monte Carlo rollouts from each step in the solution.
   대신  https://arxiv.org/pdf/2312.08935의 접근 방식을 적용하여, 각 단계에서의 Monte Carlo 롤아웃을 실행하여 얻은 단계별 정확성 추정치( per-step correctness  )를 사용해 PRMs을 human 라벨링 없이 감독한다.
2. Our PRM’s per-step predictions therefore correspond to value estimates of reward-to-go for the base model’s sampling policy, similar to recent work [31, 45].
   따라서 우리의 PRM의 단계별 예측은 기본 모델의 샘플링 정책에 대한 향후 보상의 가치 추정치에 해당하며, 이는 최근 연구 [31, 45]와 유사하다.
3. We also compared to an ORM baseline (Appendix F) but found that our PRM consistently outperforms the ORM.
    ORM 기준선과도 비교했지만 (부록 F), PRM이 ORM보다 일관되게 뛰어나다는 것을 발견했다.
4. Hence, all of the search experiments in this section use a PRM model.
   따라서 이 섹션의 모든 검색 실험은 PRM 모델을 사용한다.
5. Additional details on PRM training are shown in Appendix D.
   PRM 훈련에 대한 추가 세부 사항은 부록 D에 나와 있다.

Answer aggregation

 

5.2. Search Methods Against a PRM

6. Refining the Proposal Distribution

 

Simply prompting existing LLMs to correct their own mistakes tends to be largely ineffective for obtaining performance improvements on reasoning problems (LLM cannot self correct reasoning yet)

LLM의 자기 스스로 잘못을 고치기 위해 프롬프팅을 변형하는 것은 성능향상에 비효율적인 경향이 있다

 

Therefore, we build on the recipe prescribed by Recursive introspection

따라서 recursive introspection 논문의 방법론에

 

,incorporate modifications for our setting, and finetune language models to iteratively revise their own answers

미세조정된 LM과 modification을 합친다

 

We first describe how we train and use models that refine their own proposal distribution by sequentially conditioning on their own previous attempts at the question. We then analyze the inference-time scaling properties of revision models

먼저 우리는 모델이 자신의 이전 시도를 conditioning on해 proposal distribution을 개선하는 방법을 학습하고 사용하는 방식을 설명한다. 그런 다음, 수정 모델의 inference-time 스케일링 properties를 분석한다.

 

• Generating revision data.
  revision 데이터 생성.
• The on-policy approach of Qu et al. [28] for obtaining several multi-turn rollouts was shown to be effective, but it was not entirely feasible in our infrastructure due to compute costs associated with running multi-turn rollouts.
  여러 회차 롤아웃을 얻기 위한 on-policy 접근 방식이 효과적이라는 것이 입증되었지만, multi-turn 롤아웃 실행과 관련된 계산 비용 때문에 우리의 인프라에서는 완전히 실현 가능하지 않았다.
• Therefore, we sampled 64 responses in parallel at a higher temperature and post-hoc constructed multi-turn rollouts from these independent samples.
  따라서, 우리는 더 높은 온도에서 64개의 응답을 병렬로 샘플링하고, 이러한 독립 샘플들로부터 사후적(post-hoc)으로 multi-turn 롤아웃을 구성했다.
• Specifically, following the recipe of [Training revision models with synthetic data. Coming soon, 2024], we pair up each correct answer with a sequence of incorrect answers from this set as context to construct multi-turn finetuning data.
  구체적으로, [1]의 방법을 따라, 우리는 이 집합에서 각 정답을 일련의 잘못된 답변과 짝지어 multi-turn 파인튜닝 데이터를 구성하기 위해 문맥으로 사용했다

 

• We include up to four incorrect answers in context, where the specific number of solutions in context is sampled randomly from a uniform distribution over categories 0 to 4.
  문맥에 최대 네 개의 잘못된 답변을 포함하며, 문맥에서의 특정 답변 수는 0에서 4까지의 범주에서 균일 분포로 무작위 샘플링된다.
• We use a character edit distance metric to prioritize selecting incorrect answers which are correlated with the final correct answer (see Appendix H).
  우리는 character eidt distance 메트릭을 사용하여 최종 정답과 상관이 있는 잘못된 답변을 우선 선택한다 (부록 H 참조).
• Note that token edit distance is not a perfect measure of correlation, but we found this heuristic to be sufficient to correlate incorrect in-context answers with correct target answers to facilitate training a meaningful revision model, as opposed to randomly pairing incorrect and correct responses with uncorrelated responses.
  토큰 편집 거리가 상관관계의 완벽한 측정치는 아니지만, 우리는 이 휴리스틱이 잘못된 문맥 내 답변과 올바른 목표 답변 간의 상관관계를 충분히 맞출 수 있어 의미 있는 수정 모델을 훈련하는 데 적합하다는 것을 발견했다. 이는 잘못된 답변과 올바른 답변을 무작위로 짝짓는 것과는 다르다.

 

5. Related Work

Reward models (RMs) and verifiers.

Conventionally, RMs and verifiers are trained as discriminative models via binary classification: given a prompt and a corresponding solution or a pair of solutions), the model is either trained to predict the correctness of the solution (Cobbe et al., 2021; Lightman et al., 2023; Luo et al., 2024; Uesato et al., 2022; Wang et al., 2023; Yu et al., 2024)

분별적인 reward를 제공하는 기본적인 reward model혹은 verifier 외에도 LLM-as-a-judge 방식을 통해

or a preference between the two solutions (Nakano et al., 2021; Stiennon et al., 2020). Concretely, the RM directly produces a numerical continuous-valued score, which is then plugged into a classification objective (3). As such, discriminative verifiers do not utilize the generation capabilities of LLMs. In contrast to discriminative RMs, GenRM represents the correctness decision using the log probability of specific tokens, for example ‘Yes’ and ‘No’. Posing verification as generating “yet another token” allows it to tap better into the generation capabilities of LLMs, by making it straightforward to employ CoT reasoning and additional inference-time compute for better verification. LLM-as-a-Judge. Another line of work that poses verification as next-token prediction simply prompts off-the-shelf LLMs to act as a verifier when provided with a rubric and a template for grading (Bai et al., 2022; Kim et al., 2023; Ling et al., 2024; Zheng et al., 2024) or many-shot ICL examples (Agarwal et al., 2024), but without any specific training for the same. Perhaps unsurprisingly, we find in our experiments that using more powerful LLMs (Gemini 1.0 Pro) as a judge is worse than our trained GenRM using weaker Gemma models (Figure 1, 10), highlighting the necessity of training generative verifiers. Our generative verifiers also exhibit good out-of-distribution generalization, which might be due to better calibrated uncertainty estimates from training (Kapoor et al., 2024). More generally, even the strong proprietary LLMs, such as GPT-4 (Achiam et al., 2023) and Gemini (Team et al., 2024), fall behind trained RMs on popular leaderboards (Lambert et al., 2024), and this gap is much larger for reasoning.

 

Using CoTs for reward models. Prior works have also used critiques or CoT to extract preference and verification signals using LLM-as-a-Judge (Wang et al., 2024; Wu et al., 2024; Yuan et al., 2024); in contrast to these works, GenRM utilizes model-generated CoTs directly for training the verifier. Upon inference, a GenRM-CoT produces its own CoTs, which it then uses to make decisions on correctness, unlike Ye et al. (2024) that simply uses CoTs from a separate highly-capable LLM. In contrast to prior work that utilizes high-quality data from humans to train critique models (Saunders et al., 2022) or train discriminative RMs for generating code critiques (McAleese et al., 2024), we show that GenRM can be trained from purely synthetic, model-generated critiques. Concurrent work (Ankner et al., 2024) trains an RM to produce response critiques for preference pairs generated using a much more capable LLM, which are then passed as input into a RM head, separate from the base LLM. Unlike GenRM which uses next-token prediction, their RM head is trained discriminatively akin to standard RMs. While this approach allows them to leverage CoT, it does not allow them to unify solution generation and verification as a result of a discriminative RM head, which GenRM seamlessly enables (Section 4.2). Moreover, their synthetic critiques are not filtered for correctness, which would lead to poor verification CoTs on reasoning tasks (§3.3). Unified generation and verification. One of the hallmark properties of GenRM is that the same generative verifier can be co-trained with a generation objective (5): when given a problem, the model is trained to produce a solution, whereas when given a problem and a candidate solution, it is trained to verify this candidate. This is related to DPO (Rafailov et al., 2024) and its application to learning verifiers in reasoning (Hosseini et al., 2024), which aims to unify generation (policy) and verification (reward models) by representing the reward implicitly using the logits of a policy and training the policy with a reward-modeling loss. For reasoning, this type of model tying has been shown to exhibit erroneous extrapolation and degradation in learned representations, which prior work has attempted to address with additional techniques (Pal et al., 2024; Pang et al., 2024; Setlur et al., 2024; Yang et al., 2024). Of these, while Yang et al. (2024) train a reward model with an auxiliary generative SFT loss, note that this loss is applied on a separate head for regularization purposes and is discarded after training; unlike GenRM no text is produced when querying the RM. In addition, compared to DPO, GenRM uses a simpler next-token prediction loss, does not require a reference policy, and obtains significantly better verification performance (Figure 1, 6).