For tree-search algorithms, how to construct reliable value function and reward model is the main issue
LATS
majority voting, LLM evaluation score -> value function
simulation stage -> objective feedback == reward 실제 성공 여부로 backpropagate

예시) hotpot task
Alphamath
we have a value model V and a LLM policy model π , which are the same model but with different final layers in our paper
preliminary

method


In our case, we follow a trade-off rollout strategy between AlphaGo [32] and AlphaGo Zero [33]. Because our tree depth is much shallower than Go games (e.g., a maximum depth of 8) and expansions can easily reach a terminal node, we set an indicator function λ = Iterminal(st). If the expanded node is terminal, the reward is returned; otherwise, the value is predicted by the model V


TS-LLM
LLM-based value function v(s) conditioned on state s and learned final-step outcome reward model

LE-MCTS
We do not expand fully-expanded nodes that meet any of the following criteria:

we do not perform any rollouts. Instead, we directly employ the process-based reward model (PRM) to compute the reward. 이때 사용하는 PRM = Math Shepherd
One advantage of performing rollouts in our setup is that it enables the use of an outcome-based reward model (ORM) to compute the reward. However, as demonstrated by Uesato et al. (2022), both PRM and ORM emulate process-based feedback and achieve similar performance. Therefore, we decide not to perform rollouts, as the performance improvement with ORM is minimal, while the execution time increases by approximately five to tenfold.

기존의 backpropagation이 아닌 optimistic backpropagation

ReST-MCTS*
value model 다양
MC-rollout 존재
alphago and TS-LLM use a simplified three-stage iteration that doesn’t include a simulation process on leaf nodes. In contrast, we believe that a simulation process still brings about useful information for value estimation, despite the rise in generation and time cost. In this stage, we propose to simulate a few steps upon the new node C_i with maximum predicted value. Reasoning steps starting from this node will be sampled step-by-step and evaluated, while only the most valuable path is further explored, until a step limit m is reached. The highest quality value acquired in the sampling process v_max is recorded and used to update v_{C_i} with a weight parameter α following



rStar-math'
Q-value assignments 진행 -> PPM 사용 process preference model
q(s) is provided by the PPM
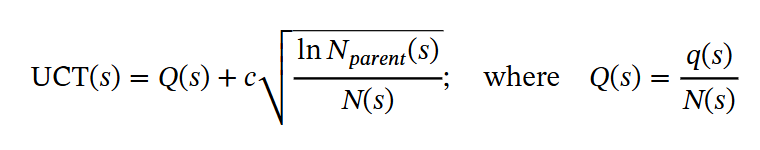
Extensive Rollouts for Q-value Annotation.
Accurate Q-value Q(s) annotation in Eq. 1 is crucial for guiding MCTS node selection towards correct problem-solving paths and identifying high-quality steps within trajectories. To improve Q-value reliability, we draw inspiration from Go players, who retrospectively evaluate the reward of each move based on game outcomes. Although initial estimates may be imprecise, repeated gameplay refines these evaluations over time. Similarly, in each rollout, we update the Q-value of each step based on its contribution to achieving the correct final answer. After extensive MCTS rollouts, steps consistently leading to correct answers achieve higher Q-values, occasional successes yield moderate Q-values, and consistently incorrect steps receive low Q-values. Specifically, we introduce two self-annotation methods to obtain these step-level Q-values. Fig. 1(c) shows the detailed setting in the four rounds of self-evolution.
두가지로 나뉨 terminal guided annotation, ppm guided annotation


FoT
는 MCTS가 아닌 score 를 주고 top-k 몇개씩 pruning하는 sparse activation 방식 + self-correction 시도
Mulberry(CoMCTS)
여러개의 MLLM을 프롬프트를 이용해 얻은 점수로 reward로 사용
Simulation and Error Positioning.

backpropagation 식
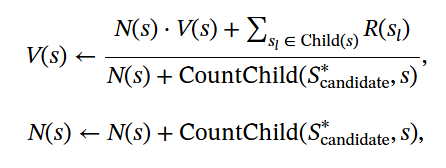
UCB value 식

그 외로는 negative sibling node에 대한 reflection through prompting by LLM
AStar
In this paper, we utilize off-the-shelf ORM model: Llama3.1-8B-ORM-Mistral-Data (?) 모순
reward value in MCTS
To simplify the construction of thought cards via the MCTS iteration, we avoid introducing an external reward model to score each step. Given the current skepticism regarding the self-rewarding capabilities of language models, alternative methods are necessary. Inspired by the principle that actions leading to correct answers should be rewarded more frequently, we aim to increase their likelihood of selection in future MCTS tree expansions. Following Zhou et al. (2024); Wu et al. (2024a), we define the reward value as the likelihood (or confidence) of self-consistency via majority voting. Note that this principle applies only to leaf nodes. The Q-values of intermediate nodes are initially set to 0 and are dynamically updated during the backpropagation process, as described in Equation 1.
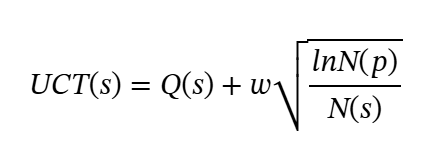
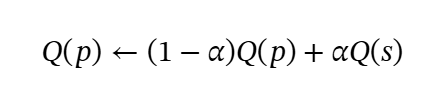
Preliminaries
Q구하는 법 : self-consistency checks or outcome reward models. 등이 있는데
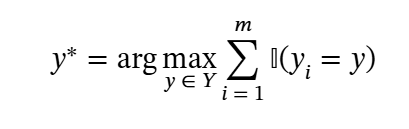
self-consistency의 경우
simple but effective approach
하지만 for complex reasoning tasks where models may only achieve correct reasoning with low probability, simple self-consistency might not provide stable performance.
PRM,ORM의 경우
Recent advances in LLM reasoning verification have demonstrated significant improvements in reasoning capabilities through verification modules
하지만. However, the scarcity of multimodal supervision data and challenges in ensuring supervision signal quality often -compromise verification effectiveness, with few high-performance open-source verification models currently available.
-------------------->
Therefore, for simplicity, we leverage mature text-domain outcome reward models (ORM).
To leverage these powerful text-domain verification models for visual reasoning while maintaining our principle of balancing performance and efficiency, we directly employ an MLLM to translate the original visual problems into pure text format.
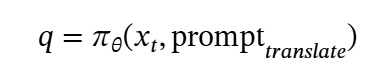
where prompt_translate denotes a translation prompt (e.g., “please translate the question and visual image into a pure text format”). The resulting text question q and the derived language-based reasoning steps derived from prior visual reasoning are then jointly processed by the ORM model for path selection and verification.
추가적인 사항- 일종의 pruning
In the MCTS-powered prior thought card construction stage, we implement an early termination strategy based on self-consistency Wang et al. (2023) for enhanced efficiency. Building on the observation that repeated action sampling at the same state often indicates successful task completion, we terminate simulation early when the model’s consistency score exceeds a threshold c (i.e., SC(s)>c).
AR-MCTS
Inference. During the inference phase of AR-MCTS, we utilize the fine-tuned PRM to follow the steps of AR-MCTS in Figure 3, employing the PRM scores as the value for each step in the evaluation phrase.
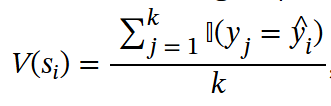
where k, 𝕀 denotes the number of sampled reasoning paths and the indicator function. If the final answer y equals the grounding truth yhat, we set the value of the current node to 1; Otherwise, we set it to 0.
MCTS performs a backward update of the visit count and Q-value for each (s,a) along the route from the current node to the root, which is fomulated as
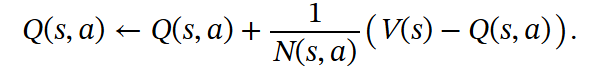
After acquiring step-wise reasoning annotations, we draw inspiration from curriculum learning [94, 23] to design a two-phase approach for PRM

1,즉 y가 gt일때 r은 sigmoid score(r) 임으로 1에 가까워지도록 그래야 log1 은 0이되니까 r의 값이 커진다
0, 즉 오답일때 r은 매우 작아진다 그래야 sigmoid(r)이 0이 되어 loss가 없어짐으로