https://arxiv.org/abs/2406.14283
LLM의 auto regressive 과정은 '시스템 1' 로 특징지을 수 있는데
이는 빠르고 본능적이지만 정확도가 떨어지는 사고 방식으로
최근의 연구들은 주로 프롬프팅, 파라미터 조정, reward 모델 훈련으로 LLM의 '시스템 1' 능력을 향상시키는 데 초점을 맞추고 있다:
반면, 복잡한 추론 문제를 해결하기 위해서는 더 심층적이고 신중하며 논리적인 사고 단계,
즉 '시스템 2' 모드가 필요하다.
수학 문제 해결을 예로 들면, 잘못된 중간 추론 단계 (예: 계산 오류, 잘못된 해석)는 잠재적으로 최종 답변의 오류로 이어질 수 있다.
'시스템 2' 추론 능력을 향상시키기 위한 이전의 시도 에는 기본적인 트리 검색 알고리즘 (ToT), MCTS, A* 등을 사용한 심층 사고가 포함되는데
이러한 방법들에서 사용되는 유틸리티 함수는 각 특정 작업에 대해 설계하는 데 많은 전문 지식이 필요하며, 새로운 시나리오로 확장하기 어렵다
llm의 multi-step reasoning을 MDP(markov decision process)로 생각
기존의 ToT, A*, MCTS의 LLM의 적용은 (reasoning capability를 올리기 위한) utility function에 LLM의 피드백을 사용했기에 정확하지 않을 확률이 높고, 각각의 task에 specific 하다. 또한 MTCS의 rollout의 경우 디코딩 시간을 매우늘리는 등의 단점이 명확하다
이를 위해 Q*는 LLM의 가장 정확한 reasoning step을 선택하기 위한 Q-value 모델을 제시한다
수학, 코드 작성, agent에서의 planning에는 multi-step reasoning이 매우 중요하다
input을 question, q라 할때 output은 single-step reasoning T개의 연속된(concat) 시퀸스로 생각될수 있다. 이 각각의 step은 한 줄일수도 또는 정해진 토큰의 개수일수도있다
특정 timestamp t에서의 상태, state s 는 따라서

이렇게 표현될 수 있다.
reward function 을통해 질문이 얼마나 잘 해결됬는지를 평가하는데 이를
final answer을 ground truth와 비교를 통해 보상을 측정한다

따라서 최종의 Q function은 discount factor 감마와 위의 reward 를 고려한 formula로

최적의 정책(LLM) 일 때 Q function을 optimal Q-function 그리고 이는 Bellman optimality equation:를 만족한다

A* 알고리즘
누적 경로 비용 accumulated path cost = g(n)
최단 경로 비용 heuristic value that estimates the cost of the shortest path from n = h(n)
f(n) = g(n) + h(n),
이 f(n)이 최소가되는 경로를 찾는다
Q*
이 A*의 f() 을 state, 즉 f(state)로 해서
g(st)는 초기 상태 s1에서의 총 utility을 나타내며, h(st)는 st에서 올바른 답변에 도달할 확률을 측정하는 휴리스틱 값을 나타낸다


Agg는 보상들을 집계하는 함수로, 가능한 것은 min, max, sum, [−1] 등이 있다.
- min: 최소 보상
- max: 최대 보상
- sum: 보상의 합
- [−1]: 마지막 상태의 보상을 총 효용으로 사용
이를 통해 초기상태에서 t까지의 reward를 요약(summarize)
R^p( process-based reward function )은 - PRM
다음과 같은 방법으로 학습될 수 있습니다:
- 인간 피드백: 인간이 제공하는 피드백을 통해 학습
- 실제 데이터: 실제 정답 데이터를 사용하여 학습
- 규칙: 미리 정의된 규칙을 사용하여 학습
- 추론 단계의 로짓: 로짓(logits)은 LLM(대형 언어 모델)의 추론 단계에서의 신뢰도를 반영

따라서 최종 f value는 이렇게 구해진다

모든 가능한 다음 reasoning step를 열거하는 것은 실행 불가능(intractable)하므로
실제로는 LLM이 생성 모든 단계 후보(all step candidates) 중 상위 K개의 alternatives으로 제한한다. 따라서 식 (6)은
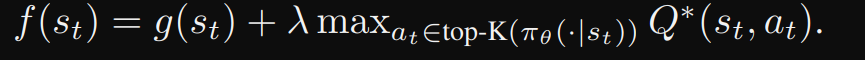

실행
Q*를 구현하는 데 있어 중요한 과제는 주어진 추론 문제에서 suboptimal일 수 있는 고정된 LLM 정책 πθ 로 상태-행동 쌍의 최적 Q-값을 estimate하는 것
LLM은 frozen되므로
따라서 데이터셋 D에서 최적 Q를 근사하는 proxy Q-값 모델을 학습


오프라인 강화 학습
오프라인 데이터셋 D가 주어졌을 때, Fitted Q-iteration 을 사용하여 proxy Q-값 모델 Q_hat를 학습
구체적으로, 각 iteration마다 Q-값 라벨은 다음과 같다
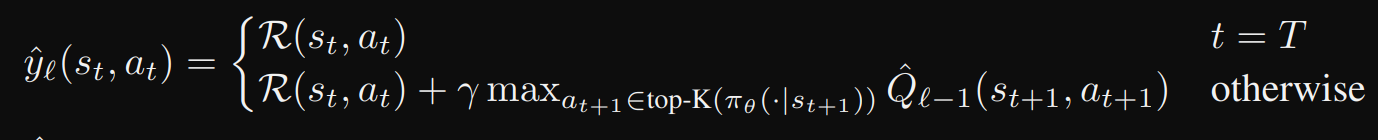
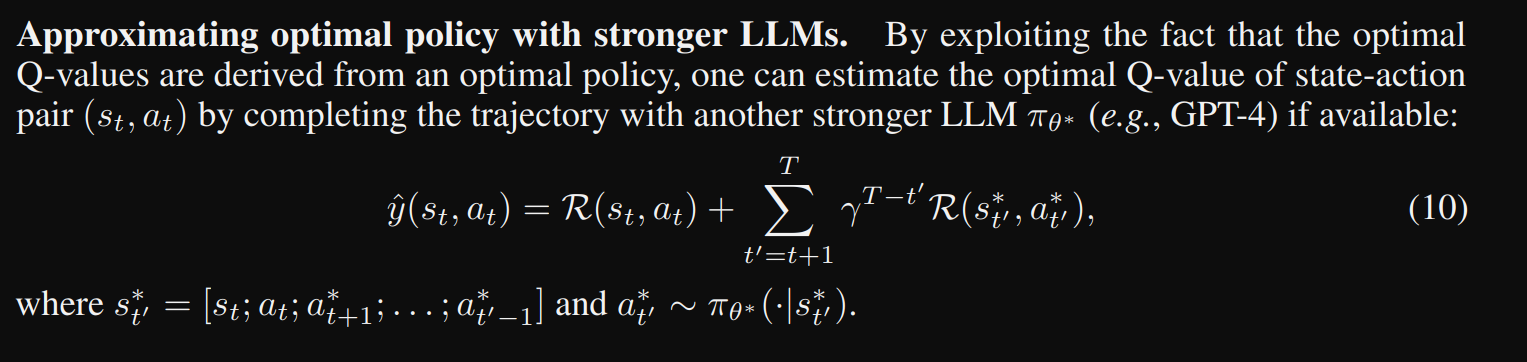
일단 이렇게 Q value 모델을 얻으면, 이를 f(n) 을 계산하는 데 사용할 수 있다. 그런 다음 A* 알고리즘을 사용하여 최상의 경로를 탐색한다. 알고리즘 1은 심의 계획 과정을 설명
- 초기화: 탐색할 상태 후보를 저장하는 집합 unvisited는 입력 질문 만 포함하고, 방문한 상태를 기록하는 집합 visited\text{visited}를 초기화합니다.
- 탐색 과정: 매 단계에서 ff-값이 가장 큰 상태 ss를 선택하고, LLM 정책 πθ\pi_\theta로부터 top-K 대안을 쿼리하여 확장합니다.
- 업데이트: 두 집합 visited\text{visited}와 unvisited\text{unvisited}를 업데이트하고, 이 과정을 종결 상태(완전한 경로)에 도달할 때까지 반복합니다.
- 결과 추출: 최종 상태 ss의 답변 부분을 결과로 추출합니다.
이러한 방식으로 최적의 Q-값을 근사하고, 이를 사용하여 추론 문제를 해결하는 최적의 경로를 찾습니다.

detail
gssm8k 수학 데이터셋의 경우
aggregation으로 min
reward 측정을 위해 process reward model, PRM800K으로 훈련된 PRM 사용
LLM의 생성해낸 한줄을(line)을 action으로 생각
f(state) 값 계산시 discount factor, λ = 1
각각의 step마다 K = 6으로 확장
rollout으로부터 훈련하는게 가장 효율적인 방법으로
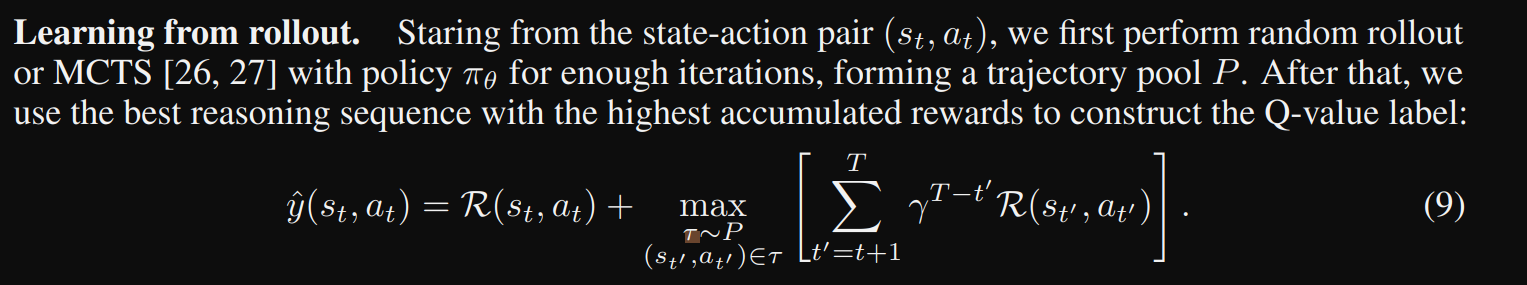
수학적 reasoning에는 τ = 0.9, 코드 생성에는 τ = 0.2 사용(temperature)를 사용해 완전한 (trajectory)를 얻고 이를 "/n"을 이용해 각각의 trajectory를 일련의 state로 분할한다
즉 LLM을 사용하여 랜덤 롤아웃 또는 MCTS를 수행하여 trajectory Pool P를 수집하고, 누적 보상이 가장 높은 최상의 reasoning path를 선택하여 현재 state-action 쌍의 해당 Q-값 label을 구성 (Q value model 데이터셋으로 사용)
보상 R(state, action)은 생성된 수학적 수치 답변이 정확하거나 프로그래밍 코드가 모든 테스트 케이스를 통과한 경우에만 1로 주어지는데
이는 state-action 쌍의 Q 값이 정확한 답변을 포함하는 trajectory을 생성할 잠재력, 즉 능력이 있는 경우에만 1이 될 수 있음을 나타낸다.
실제 GSM8k에서의 Q* 성능
