Nearest Neighbor Normalization Improves Multimodal Retrieval 논문리뷰

https://arxiv.org/pdf/2410.24114

https://github.com/multimodal-interpretability/nnn

GitHub - multimodal-interpretability/nnn: Nearest Neighbor Normalization (EMNLP 2024)

Multimodal models leverage large-scale pretraining to achieve strong but still imperfect performance on tasks such as image captioning, visual question answering, and cross-modal retrieval.

In this paper, we present a simple and efficient method for correcting errors in trained contrastive image-text retrieval models with no additional training, called Nearest Neighbor Normalization (NNN).

We show an improvement on retrieval metrics in both text retrieval and image retrieval for all of the contrastive models that we tested (CLIP, BLIP, ALBEF, SigLIP, BEiT) and for both of the datasets that we used (MS-COCO and Flickr30k).

NNN requires a reference database, but does not require any training on this database, and can even increase the retrieval accuracy of a model after finetuning.

 

1. Introduction

 

Contrastive image and text models are a fundamental building block of large-scale text-to-image or image-to-text retrieval systems (Radford et al., 2021; Jia et al., 2021; Zhang et al., 2022).

These models utilize contrastive loss functions to learn joint text and image embeddings, aligning embeddings for matching text and image pairs while separating embeddings for non-matching pairs.

However, contrastive embeddings optimize pretraining objectives such as InfoNCE (Radford et al., 2021) rather than downstream retrieval accuracy, so learned embeddings can be suboptimal for retrieval (Zhou et al., 2023).

Many methods for improving contrastive models on downstream retrieval tasks require additional training to adapt models across domains or aggregate information from an external database (Zhou et al., 2022; Singha et al., 2023; Iscen et al., 2023), and others are specialized for individual error categories, such as gender bias (Wang et al., 2021, 2022a; Berg et al., 2022).

 

Recent training-free methods suggest that accuracy can be improved without fine-tuning, which is useful for limited-compute environments and critical for black-box embedding models.

Such methods typically use a reference database of query and retrieval embeddings to adapt the pretrained model to the downstream retrieval task.

For instance, QBNorm and DBNorm normalize scores for each retrieval candidate by computing a softmax over the entire reference database (Bogolin et al., 2022; Wang et al., 2023).

These approaches mitigate the hubness problem, where certain retrieval candidates ("hubs") emerge as nearest neighbors for many queries in high-dimensional embedding spaces, leading to incorrect matches (Radovanovic et al., 2010).

These methods tend to be computationally impractical, requiring match score calculations for every item in the database and thus scaling linearly with the size of the reference database.

Distribution normalization (DN) reduces complexity to constant time by using a first-order approximation of softmax normalization (Zhou et al., 2023): text and image embeddings are normalized by subtracting the mean reference embedding.

While DN is much faster than QBNorm and DBNorm, this practicality comes at the cost of reduced retrieval accuracy.

Can sublinear runtime be achieved without sacrificing accuracy?

 

In this paper, we introduce Nearest Neighbor Normalization (NNN), a novel training-free method for contrastive retrieval (Figure 1).

Like DN, it adds minimal inference overhead with sublinear time complexity relative to the reference database size—but it also outperforms both QBNorm and DBNorm on retrieval.

The key idea is that NNN corrects for the effects of embeddings that are assigned disproportionately high or low retrieval scores, by normalizing per-candidate scores using only the k closest query embeddings from a reference dataset.

For example, NNN reduces scores for the image of the surfer in Figure 2 (a hub that incorrectly matches a large number of query captions), improving overall accuracy.

Section 2 provides more details on our approach, and Section 3 empirically validates the effect of NNN for a range of models and datasets.

Overall, we contribute a new and conceptually simple approach for improving contrastive retrieval with little compute overhead.

In addition to improving retrieval scores consistently for every model and dataset that we tested, NNN can reduce harmful biases such as gender bias.

 

2 Nearest Neighbor Normalization

Retrieval models compute a match score s(q, r) between a query q and database retrieval candidate r, and return the highest-scoring candidates.

In the case of contrastive multimodal models such as CLIP, this score is typically the cosine similarity between image and text embeddings (Radford et al., 2021).

Figure 2 shows how the hubness problem (Radovanovic et al., 2010) manifests as a failure mode of contrastive text-to-image retrieval.

Some images are simply preferred by contrastive models over other images: they have high cosine similarity with a wide array of query captions.

To correct for bias towards hubs in image-text retrieval, we propose NNN, an approach that estimates bias for each retrieval candidate using a database of reference queries, D.

The bias is then applied as an additive correction to the original match score, then used for retrieval.

Specifically, given a contrastive retrieval score s(q, r) = q·r, we define the bias b(r) for a retrieval candidate r as a constant multiple (α) of the mean of s(q1, r), s(q2, r), . . . , s(qk, r), where {q1, . . . , qk} = D_top k(r) are the k queries from the reference query dataset that have the highest similarity score s(q_i , r) with r.

Namely, if we define the operator argmaxk to denote thek arguments for the which a function attains its k maximum values,

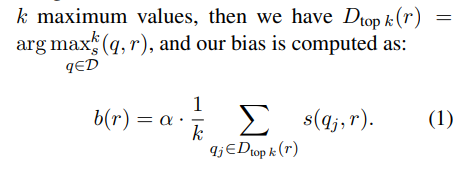
NNN uses the nearest k query embeddings to differentiate similar objects, capturing fine-grained distinctions between retrieval candidates. Each retrieval candidate has a constant bias score, so these scores can be computed offline and cached. The debiased retrieval score can then be computed by subtracting the estimated bias from the original score:

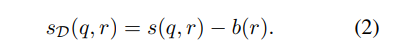
When using vector retrieval to compute match scores, bias scores are computed in sublinear time and add a constant factor to retrieval runtime; see Section 3.1 for further discussion.