https://arxiv.org/pdf/2409.15254

Archon:
An Architecture Search Framework for Inference-Time Techniques
논문리뷰
2024년 10월 1일자 논문
challenge
1) inference-time compute budge에 관한 최적의 컴퓨팅량
2) 다양한 inference-time 기술 사이의 interaction에 대한 이해
3) model choice의 큰 공간(범위)을 효율적으로 search해 best 답변을 내놓기
에 대한 challenge가 존재 아직
task
instruction-following tasks (MT Bench, AlpacaEval 2.0, Arena-Hard-Auto)
reasoning tasks (MixEval, MixEval-Hard, MATH)
여러 기술들 포함한 design space
generative
1. generation ensembling
2. multi-sampling,
reductive
3. ranking
4. fusion
comparative
5. critiquing
6. verification
7. unit testing

3.1 LLM Components of Archon
Generator: (repeated sampling : LL monkey, more llm calls are all you need 논문, generation ensembling (MoA)
LLM that creates candidate responses
Fuser: (Mixture of agents의 aggregator와 동일 역할)
LLM that combines multiple candidate responses to create one or more higher-quality responses
Ranker:
language model that ranks the current list of candidate generations based on their quality and the instruction prompt
Critic: (self-taught evaluator, self-rewarding llm 논문, 그외로는 self-refine, reflexion, CRITQUE?, llm critique help catch bug 논문)
LLM that produces a list of strengths and weaknesses for each candidate response in a provided set
Verifier: (generative verifier, OmegaPRM 논문등 reward model관련 논문들)
LLM that verifies whether a provided candidate response has appropriate reasoning for a given instruction prompt
Unit Test Generator: ( @pass k? 논문)
LLM that generates a set of unit tests for a given instruction prompt.
As input, the unit test generator solely takes in an instruction prompt. As output, the unit test generator produces a list of unit tests that are consequential for the accuracy and relevance of a candidate response
Unit Test Evaluator:
language model that evaluates each candidate generation against a generated set of unit tests
As input, the unit test evaluator takes in the instruction prompt, candidate response(s), and set of unit tests. As output, the unit test evaluator outputs the candidate response(s), ranked in descending order by how many unit tests they pass. We use model-based unit test evaluation by prompting the LLM to provide reasoning and verdicts for each unit test across each of the candidate responses.

component을 조합한 archon architecture 예시
rule
1. only one module, 즉 componenet can be present in 주어진 레이어
2. generator 요소는 must and can be placed in 첫번째 레이어
3. critique 요소 must come before ranker 또는 fusion 요소 - 생성된 weakness, strength가 incorporate하기 위해
4. Unit Test Generators 와 Evaluators 요소는 반드니 placed in layer next to each other

One contributing factor is that, unlike the distribution of instruction-following/reasoning tasks, coding tasks tend to have one or two LLMs that perform substantially better than the rest of models (Table 14).
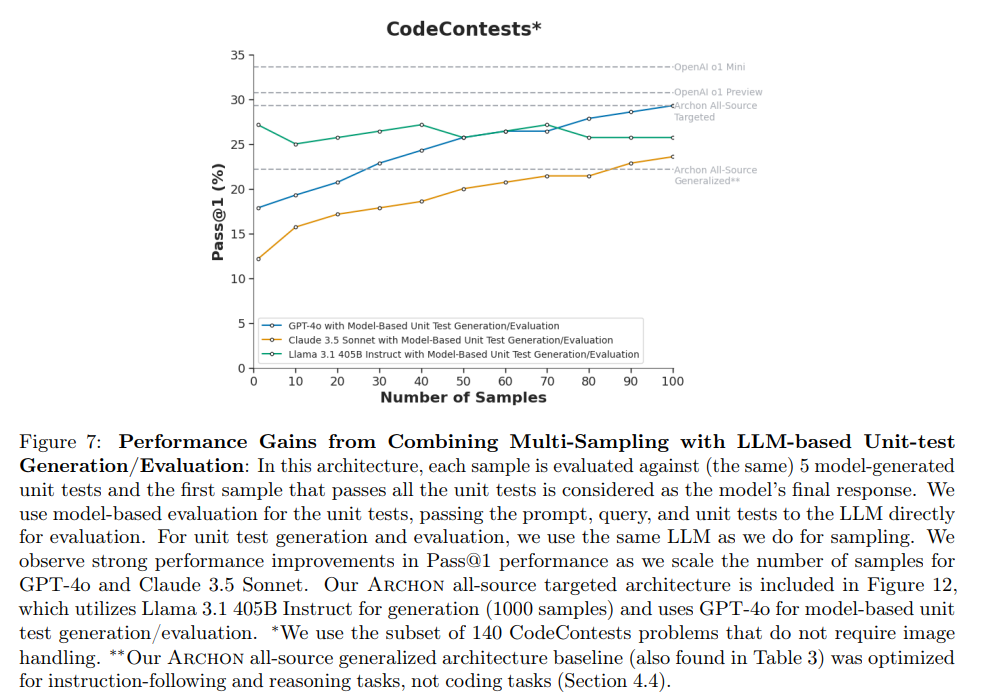
However, when we add unit test generation/evaluation, and increase the number of samples, Archon’s performance on CodeContests improves significantly (Figure 7), allowing us to boost GPT-4o Pass@1 performance by 56% for Pass@1 (from 25 to 41 out of 140 questions).
Future work should focus on developing better Archon modules for handling the multi-step reasoning that is implemented in various code agents [generative verifier, mutual reasoning makes smaller LLMs stronger problem-solver]
3.4 Inference-Time Architecture Search (ITAS)
In this section, we explore different approaches for finding the best inference-time architecture (for a given task) through inference-time architecture search (ITAS).
Due to compute resources, we pre-filtered certain ways of combining LLM components to reduce the search space while still building effective inference-time architectures.
While it is possible to expand the search space of potential Archon architectures (e.g. different temperatures for generative LLM components, alternative prompts for each LLM component, multiple layers of Generator modules, additional LLM components for Archon, etc.),
we use our analysis from Section 3.2 to selectively limit our search space to configurations that fit our rules for Archon: starts with a layer of Generator modules, followed by layers performing fusing, ranking, critiquing, verifying, and unit testing.
Search Hyperparameters: With the studied LLM modules and their relationships within the Archon architecture, we selected five main axes for the hyperparameters in our search:
1. Top-K Generators for Ensemble: The top-K models to be used for the initial Generator ensemble, ranges from 1 to 10.
The top-K models are the best-K LLMs for the given task, based on their individual performances (Table 14).
2. Top-K Generator Samples: The number of samples gathered from each Generator in the ensemble (it is the same for all the models), ranges from 1 to 5. For MATH and Code-Contests, we also explore high sample settings over the following set of samples: [1, 10, 100, 500, 1000].
3. Number of Fusion Layers: The number of layers of Fusers, ranges from 1 to 4.
The last fusion layer will always have a single Fuser.
4. Top-K Fusers for Fusion Layers: The top-K models used for each fusion layer, ranges from 2 to 10 and increases by 2 each time.
By combining all the hyperparameters, we create a search space of 6,250 configurations by multiplying each of the configuration option counts together (10∗5∗5 (4−1) = 6250).
However, we remove configurations that are not viable: configurations in which the number of initial generations exceeds the context window of the fusers (i.e. 24 candidate generations) and configurations with only one fuser layer but multiple fusers declared.
This reduces our search space to 3192 configurations.
For these configurations, we add critic and ranker layers before each fuser layer since they’ve been shown to have added benefits across the benchmarks explored (Figure 4; Figure 5).
The ranker selects the top-5 candidate generations to send to the next layer.
Additionally, for our coding tasks (i.e. CodeContests), we use unit test generators and evaluators after our initial generation layer, with a default setting of 10 unit tests generated.
On our instruction-following and reasoning tasks (i.e. MT-Bench, AlpacaEval 2.0, Arena-Hard-Auto, MixEval, MixEval-Hard, and MATH), we also ablate adding a verifier before the final fuser layer (Table 2).
Ultimately, we could increase the search space substantially more along various other axes, such as additional combinations of verifier, unit test generation, and fuser layers, but given our compute resource limitations, we did not scale further.
Search Techniques: Within the hyperparameter space, we explored four search algorithms for automating the development of inference-time architectures:
1. Random Search: Randomly selects a combination of hyperparameters for our Archon architecture.
2. Greedy Search: Starting with a base Archon configuration, marginally changes each hyperparameter and test if it improves performance or not.
If it does, incorporate the change. If not, move on to the next hyperparameter.
3. Bayesian Optimization: Efficiently selects the most promising hyperparameter configurations for Archon by building a probabilistic surrogate model and leveraging an acquisition function for hyperparameter selection [36, 48] (Section A.5).
To get our model ranking for the benchmark, we calculate the model ranking by testing each model individually on the entire benchmark (K = 1) in the first stage of the search.

To get our fusion model ranking for the benchmark, we use the same approach, testing each model’s fusion performance with an ensemble of 10 randomly selected models from the available set.
From our experiments, we found that the best generator and fusion models could vary widely dataset to dataset, making it beneficial to perform these rankings for new datasets (Table 14).
For search, we use a 20% sample of each dataset for guiding architecture search to improve the evaluation speed while getting meaningful development signal.
Comparing Search Algorithms:
In Figure 6, we compare the effectiveness of each search algorithm on our explored benchmarks.
While random search guarantees the optimal Archon configuration, we found Bayesian optimization to be most effective in terms of tradeoff between finding the optimal configurations and minimizing the number of configurations tested.
For 95.2% percent of the search iterations tested in Figure 6, we found that Bayesian optimization had the optimal configuration amongst the four explored search algorithms.
We use 80 initial samples for our Bayes optimization architecture search (Section A.5).
Bayesian optimization also found the best architecture configuration in 80.4% less evaluations than greedy search and 87.1% less evaluations than random search.
Bayesian Optimization Analysis:
In Table 22, we explore how the number of initial testing points, the number of exploration iterations, and the Archon inference call budget impacts the effectiveness of Bayesian optimization.
Additional initial testing points continue improving search efficacy up until 80-90 samples, where testing would be better delegated towards configuration search.
For lower inference call budgets with Archon (e.g. <20 inference calls), Bayesian optimization proved less effective, performing more similarly to greedy search or random search given the limited search space (Table 23.
Therefore, Bayesian optimization is more effective for more open-ended ITAS with larger inference call budgets (e.g. >20 inference calls) whereas traditional component engineering might be better for more limited inference call budgets.
4 Experiments
In our experimental evaluations, we focus on four questions:
(1) how do Archon architectures compare to existing SOTA closed-source LLMs and other inference-time architectures?
(2) how does Archon performance compare across tasks?
(3) how does Archon performance compare when optimized for a set of tasks vs. an individual task?
(4) what are the current limitations of Archon and plans for future work?
4.1 Benchmarks and Models
In this section, we discuss the benchmarks and models used in our LLM component analysis and development of Archon. coding: MT-Bench [64], AlpacaEval 2.0 [30], Arena Hard Auto [29], MixEval [37], MixEval-Hard, MATH [20], and CodeContests [31].
We provide an overview of each dataset in Table 25, where we compare their query counts, scoring type, evaluation metrics, baseline models, and judge models.
Since we perform ITAS on a randomly sampled 20% subset of each benchmark, we evaluate on the remaining held-out 80% subset of the benchmark (Table 3) (for Archon performances on the entire benchmarks, please see Table 24).
For MixEval and MixEval Hard, we use the 2024-06-01 dataset release.
For MT Bench and Arena-Hard-Auto, we also include a configuration with Claude-3.5-Sonnet as the baseline model (in addition to the original setting with GPT-4-0314) to have a stronger model for comparing against Archon architecture performances (Table 3) and mitigate the GPT-4-Turbo judge bias towards GPT responses.
Additionally, we chose not to use the single-scoring configuration for MT Bench due to the inconsistencies in LLM judge scoring on 1-10 scales [49, 52].
For MATH, we evaluate a random sample of 200 problems from the dataset’s test set.
For CodeContests, we evaluate on the 140 test set questions that do not include image tags in the problem description.
Models:
For Archon, we test across three model categories: 8B or less parameter models, 70B or more parameter models, and closed-source model APIs.
For our 8B and 70B+ models, we selected the top-10 performing chat models for each parameter range on the Chatbot Arena Leaderboard [9] as of July 2024.
For our closed-source model APIs, we include GPT-4o, GPT-4-Turbo, Claude Opus 3.0, Claude Haiku 3.0, and Claude Sonnet 3.5.
We list and compare all of the models tested in the Archon framework in Table 13 and Table 14. 4.2 Archon vs. Closed-Source LLMs and Other Inference-Time Architectures

We start by comparing Archon architectures to existing SOTA closed-source LLMs and inference-time architectures across a set of instruction-following, reasoning, and coding tasks with either pairwise ranking or accuracy metrics, as described in Section 4.1.
Since we perform ITAS on a randomly sampled 20% subset of each benchmark, we evaluate on the remaining held-out 80% subset of the benchmark (Table 3) (for Archon performances on the entire benchmarks, please see Table 24).
Based on our results in Table 3, we find that Archon architectures consistently match or surpass existing SOTA approaches across all the benchmarks explored.
On the evaluation suite, our Archon architectures with open-source models experience a 11.2 point increase, on average, above SOTA open-source approaches; for its worst performance, our open-source Archon architectures are only 3.6% above SOTA open-source approaches on AlpacaEval 2.0.
For our Archon architectures with closed-source models, we set SOTA performance across MT Bench, Arena-Hard-Auto, MixEval, and MixEval-Hard, leading to a 15.8 percentage point increase, on average, compared to closed-source approaches.
Lastly, for approaches that use all-source models available, both open and closed-source, Archon achieves an increase of 10.9 points, on average, over existing SOTA single-call LLMs.
4.3 Archon by Task
We analyze Archon performance by task style: instruction-following tasks that use pairwise ranking for scoring, reasoning tasks that use accuracy-based metrics for scoring, and coding tasks that use Pass@1.
On instruction-following tasks like MT Bench, AlpacaEval 2.0, and Arena-Hard-Auto, open-source Archon architectures outperform current open-source baselines by 10.0 percentage points, on average, while closed-source Archon outperforms current closed-source baselines by 20.1 percentage points (Table 3).
On reasoning tasks like MixEval, MixEval-Hard, and MATH, open-source Archon architectures outperform existing open-source baselines by 2.9 percentage points while closed-source Archon architectures outperform current closed-baselines by 4.2 percentage points (Table 3).
On coding tasks (i.e. CodeContests), open-source Archon architectures match existing open-source baselines (0.2 percentage points difference) and all-source Archon architectures outperform all-source baselines by 2.5 percentage points (Figure 7).
All-source architectures of Archon outperforms existing all-source baselines by 16.1 and 3.8 percentage points, on average, for instruction-following tasks and for reasoning tasks, respectively (Table 3).
Instruction-Following and Reasoning: With Archon, multiple models used for Generators and the depth of fusion layers lead to performance boosts on instruction-following tasks, increasing the richness of responses and allowing multiple iterations for step-by-step instruction-following (Table 15).
For reasoning, while the performance boost from Archon is smaller when we consider the aggregate scores for MixEval and MixEval-Hard, we do see meaningful increases in performance when we create inference-time architectures for each individual task under MixEval and MixEval-Hard (Table 26; Table 27).
When we create individual Archon architectures for each subtask, we see 3.7 and 8.9 percentage point increases in accuracy, on average, for MixEval and MixEval-Hard, respectively.
This finding suggests that reasoning tasks (e.g. mathematics, sciences, logic) require more individualized inference-time architectures for their particular queries.
Coding: We have observed that ensembling, fusion, and ranking techniques have limited impact on CodeContests (Table 2).
For example, when we apply the general all-source architecture from Table 25 to CodeContests problems, we achieve small gains from Archon (see Figure 7).
One contributing factor is that, unlike the distribution of instruction-following/reasoning tasks, coding tasks tend to have one or two LLMs that perform substantially better than the rest of models (Table 14).
However, when we add unit test generation/evaluation, and increase the number of samples, Archon’s performance on CodeContests improves significantly (Figure 7), allowing us to boost GPT-4o Pass@1 performance by 56% for Pass@1 (from 25 to 41 out of 140 questions).
Future work should focus on developing better Archon modules for handling the multi-step reasoning that is implemented in various code agents [42, 63].
For model-based unit test generation/evaluation, we generate 5 unit tests and use the LM to evaluate each candidate response against the generated unit tests, allowing us to rank the different candidate responses. Lastly, we explored several additional benchmarks for math and code (GSM8K [11], MMLU Math [20], HumanEval [8], and MBPP [3]) but existing approaches already reach fairly high performances (>90% Pass@1)(Table 28).
4.4 Task-Specific and General-Purpose Archon Architectures
Task-Specific vs. General-Purpose:
We also compare custom Archon architectures, specifically configured to a single evaluation dataset ("Task-specific Archon Architectures"), and a generalized Archon architecture configured to handle all the evaluation datasets ("General-purpose Archon Architectures") (Table 3).
We utilize ITAS to find the generalized Archon architectures in Table 3 (subsection 3.4), maximizing performance over all of the benchmarks explored except CodeContests.
We exclude CodeContests from the generalized Archon architecture search since we found that Archon architectures for coding tasks are most effective with a different set of inference-time techniques compared to instruction-following and reasoning tasks (i.e. increased model sampling combined with model-based unit test generation/evaluation) (Section 3.2; Table 2).
For open-source models, we find that our generalized Archon architecture only lags behind the specialized Archon architectures by 3.4 percentage points, on average, across all the benchmarks, demonstrating the robustness of the Archon architecture found by the ITAS algorithms (Table 3).
We see similar gaps between the generalized and specialized Archon architectures for closed-source models (4.0 percentage points) as well as the all-source models (3.3 percentage points) (Table 3).
Insights from Architecture Construction:
We include examples of our learned effective generalized Archon architectures constructed by ITAS in Section A.3, where we breakdown the exact LM components used for constructing each architecture.
For instruction-following and reasoning tasks, we found a generalizable Archon architecture to be most effective with multiple layers of critic-ranker-fuser, chained sequentially to improve candidate generation (Figure 9).
However, the specific models chosen for these LLM components could change task by task, with some tasks benefiting from using a single SOTA closed-source LLM for all the components (e.g. Arena-Hard-Auto and MixEval) (Figure 11) whereas others benefited from a diversity of LLMs in their ensemble (e.g. MT Bench and MixEval-Hard) (Figure 9; Figure 10).
Regardless of models used, we found that scaling inference layers including critics, rankers, and fusers improved performance on instruction-following and reasoning tasks (Figure 5; Section A.3).
For instruction-following and reasoning tasks, the verifier module is more effective than the unit test generation/evaluation module for task-specific Archon architectures (Section 3.2; Table 2).
For coding tasks, we found a high-sample setting to be the most effective, with added layers of unit test generation and evaluation to boost the quality of the final candidate generation (Figure 12; Figure 7).
Overall, our findings demonstrate the benefits of scaling inference-time compute through layering of techniques, showing the importance of effectively and efficiently constructing inference-time architectures.
4.5 Archon by Inference Budget
Finally, we compare different Archon architectures across inference budgets for both open-source models and closed-source models (Table 16).
For instruction-following and reasoning tasks, we find consistent improvements in downstream performance as we scale from 1 to 50 inference calls, increasing by 14.3 percentage points, on average, across our selected evaluation benchmarks (Table 16).
However, after roughly 50 inference calls, performance gains plateau.
The results suggest that the early addition of LLM components in Archon (e.g. critic, ranker, layers of fusers) led to the most substantial gains in performance and after that, additional LLM components did not ultimately enhance the final generated response.
We see the trend most apparent for the MixEval and MixEval-Hard benchmarks, where additional layers of Critic, Rankers, and Fusers do not benefit performance beyond a 30 inference call budget (Table 16).
Notably, for math and coding tasks, we see continued improvements with additional inference calls by using generated unit tests to evaluate candidate responses, leading to a 56% increase in Pass@1 (Figure 7).
4.6 Limitations and Future Work of Archon
Parameter Count: The Archon framework is most effective with LLM with about 70B parameters or more.
When we utilize the Archon architecture with only 7B open-source models, we get a notable decrease in performance (Table 17).
The best 7B Archon configurations lag behind single SOTA (and much larger) models by 15.7% on across all the benchmarks, on average; 7B models work well for ranking but are less effective for critic and fusion.
While this is expected, as small models generally exhibit lower performance, their weaker instruction following ability is a compounding factor.
Latency and Costs: Archon is not ideal for tasks that prefer the latency of a single LLM call, such as certain consumer chatbots.
Since Archon architectures often make multiple LLM calls successively for different operations (e.g. ensembling, critiquing, ranking, fusion, etc.), it can often take 5+ more time than a single LLM call (Section A.3).
Furthermore, it can require calling multiple API endpoints for a single query, leading to increased expenditures compared to single-call LLMs (Table 18; Table 19).
Note that these increases in compute costs and latency translate to higher quality responses, and can be justified in many application domains, such as science, math, and programming, or for addressing complex customer service issues.
Archon Components: While Archon is a modular framework, allowing the easy incorporation of new LLMs, new inference-time techniques, and even tool use, we only explore seven LLM inference time techniques in our work (Section 3.1).
The addition of new techniques is a promising avenue for future research.
Furthermore, while different queries can be best suited by different Archon architectures (Table 26; Table 27), the ITAS algorithm selects the best single architecture for the evaluation set queries combined.
Future architecture search could focus on dynamic selection of components on a query-by-query basis.
5 Conclusion
This paper presents Archon, a modular framework for optimizing inference-time architectures by integrating multiple inference-time techniques, such as ensembling, ranking, fusion, critique, verification, and unit test generation.
Extensive experiments demonstrate that Archon consistently matches or exceeds the performance of leading closed-source LLMs, such as GPT-4 and Claude-3.5-Sonnet, while only using open-source models across diverse benchmarks, including MT-Bench, AlpacaEval 2.0, Arena-Hard-Auto, MixEval, MixEval-Hard, MATH, and CodeContests.
We attribute Archon’s boost in benchmark performance to two main factors.
The first factor is the ability to leverage inference-time compute towards utilizing multiple LLMs and additional operations (e.g. fusing, ranking, critiquing, verification, unit testing), leading to amplified benefits that scale with additional inference calls (Sections 3.1 and 3.3).
The second factor is the automatic approach for iteratively testing different Archon architectures with ITAS, guaranteeing the optimal configuration given enough exploration steps (Section 3.4).
These results underscore the potential of Archon and ITAS algorithms in advancing the development of high-performing and generally capable inference-time architectures.
The framework and datasets are publicly available on Github: https://github.com/ScalingIntelligence/Archon.