https://arxiv.org/pdf/2407.08739
Multi-modal Large Language Models (MLLMs) have recently emerged as a significant focus in academia and industry.
Despite their proficiency in general multi-modal scenarios, the mathematical problem-solving capabilities in visual contexts remain insufficiently explored.
We identify three key areas within MLLMs that need to be improved: visual encoding of math diagrams, diagram-language alignment, and mathematical reasoning skills.
This draws forth an urgent demand for large-scale, high-quality data and training pipelines in visual mathematics.
In this paper, we propose MAVIS, the first MAthematical VISual instruction tuning paradigm for MLLMs, involving a series of mathematical visual datasets and specialized MLLMs.
Targeting the three issues, MAVIS contains three progressive training stages from scratch.
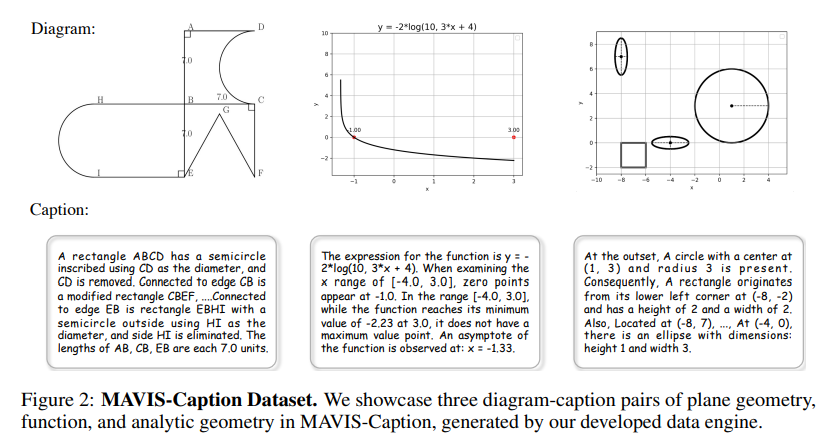
First, we curate MAVIS-Caption, consisting of 558K diagram-caption pairs, to fine-tune a math-specific vision encoder (CLIPMath) through contrastive learning, tailored for improved diagram visual encoding.
Second, we utilize MAVIS-Caption to align the CLIP-Math with a large language model (LLM) by a projection layer, enhancing vision-language alignment in mathematical domains.
Third, we introduce MAVIS-Instruct, including 900K meticulously collected and annotated visual math problems, which is adopted to finally instruct-tune the MLLM for robust mathematical reasoning skills. In MAVIS-Instruct, we incorporate complete chain-of-thought (CoT) rationales for each problem, and minimize textual redundancy, thereby concentrating the model towards the visual elements. Note that both our new datasets span a broad range of math subjects to ensure comprehensive capabilities, including plane geometry, analytic geometry, and function. On various mathematical benchmarks, e.g., MathVerse, MAVIS-7B achieves leading performance among open-source MLLMs, surpassing other 7B models by +11.0% and the second-best LLaVA-NeXT (110B) by +3.0%, demonstrating the effectiveness of our approach. Data and Models are released at https://github.com/ZrrSkywalker/MAVIS
3 Mathematical Visual Dataset In Section 3.1, we first illustrate the methodology of our data engine to automatically generate math diagrams. Then, we respectively introduce the two datasets we newly curated for MLLMs, i.e., MAVIS-Caption in Section 3.2 and MAVIS-Instruct in Section 3.3. 3.1 Data Engine To cope with the substantial data requirements of MLLMs, it is essential to have access to hundreds of thousands of training instances. However, for visual mathematics, the paucity of publicly available datasets poses a challenge, and creating such data manually is also not feasible due to the high cost involved. Therefore, we develop an automatic data engine to generate high-quality math diagrams efficiently, as showcased in Figure 1. Covering most mathematical scenarios, we adopt three diagram types: plane geometry, analytic geometry, and function. Note that all the logic of the data engine is implemented in Python, and we employ Matplotlib for the graphical rendering of the diagrams. Plane Geometry Diagram. As such diagrams typically consist of spatial combinations of various basic shapes, we utilize principles from multi-hop data curation to develop customized generation rules. These rules allow for the iterative integration of new shapes into existing configurations. Initially, we establish a core set of shapes, including squares, rectangles, triangles, sectors, etc, for diagram generation. Starting with a randomly selected shape, we extend another shape from the set along one of its straight sides. By iterating this process, we can construct diverse plane geometry diagrams featuring different combinations of shapes. Additionally, we randomly label the vertices with letters (e.g., A, B, C) and annotate numerical values relevant to geometric properties (e.g., side lengths and angles), simulating realistic plane geometry problems. Analytic Geometry Diagram. Likewise, our approach begins by defining a basic figure set that differs slightly from that used in plane geometry; for example, we include additional elements such as points and line segments. We then construct a Cartesian coordinate system, complete with grid lines and scaled axes. The range of the coordinate system is randomly determined within a predefined scope. Subsequently, we select a number from 1 to 3 to indicate the number of figures to be drawn on the graph, and randomly choose coordinates for the top-left vertices to plot these figures at varied sizes (using these points as centers for circles). Unlike plane geometry, we ensure that the figures do not overlap, except for points and segments, and maintain the figure areas within a suitable scale.
Function Diagram. We focus on seven fundamental function types: polynomial, sine, cosine, tangent, logarithmic, absolute value, and piece-wise polynomial functions. For each function type, we parameterize the equations with random variables, such as coefficients and constants within a predefined range (e.g., a and b in y = ax + b), which facilitates the generation of diverse function graphs. We also adopt the same Cartesian coordinate system employed for analytic geometry. Additionally, for specific caption or question-answering samples, we also plot key features like extreme points and zero points of the functions, providing additional visual information that aids in the understanding and reasoning of these mathematical functions. 3.2 MAVIS-Caption With our mathematical visual data engine, we first curate a diagram-caption dataset, MAVIS-Caption, as shown in Figure 2, aiming to benefit the diagram visual representations and cross-modal alignment. Data Overview. As presented in Table 1, the MAVIS-Caption dataset comprises 588K diagramcaption pairs. This includes 299K for plane geometry, 77K for analytic geometry, and 212K for function. The average word length of the captions is 61.48 words, reflecting their detailed descriptive nature. The overall vocabulary size is 149, indicating the diversity in language expression. Caption Annotation. We adopt different strategies to generate captions for three types of diagrams. Note that all the curated captions are refined by ChatGPT [50] at last for a human-like expression. • Plane Geometry Caption. We follow the iterative geometric generation process to develop regulations for an accurate and detailed caption. We first prompt GPT-4 [48] to create three sets of language templates: the descriptive content for fundamental shapes (e.g., “A Triangle {} with two congruent sides {} and {}”), the phrases to denote specific attributes (e.g., “Angle {} measures {} degrees”), and the conjunction to link two adjacent shapes (e.g., “Attached to edge {} of shape {}, there is a {}”). Then, based on various generation scenarios, we fill and merge these templates to acquire a coherent description of the geometric figure. • Analytic Geometry Caption. We also employ GPT-4 to obtain two sets of language templates: the description of coordinates and attribute information for basic figures (e.g., “The square with its base left corner at {} features sides of {} in length”) and the spatial relation for nearby figures (e.g., “On the bottom right of {}, there is a {}”). The captions are then formulated by filling in the coordinates and selecting appropriate spatial relationship templates through coordinate comparison. • Function Caption. As function diagrams typically showcase a single curve, we directly utilize GPT-4 to generate templates describing various properties of functions, including expressions, domains, ranges, extreme points, and zero points. Each template is then filled based on specific cases, such as “


3.3 MAVIS-Instruct Besides the diagram-caption data for cross-modal alignment, we curate MAVIS-Instruct of extensive problem-solving data to endow MLLMs with visual mathematical reasoning capabilities, as shown in Figure 3. Data Overview. As illustrated in Table 2, the MAVIS-Instruct dataset consists of a total of 834K visual math problems. Given that the proportion of analytic geometry problems is relatively small, we classify them with function problems for simplicity. Each problem in MAVIS-Instruct includes a CoT rationale providing step-by-step solutions, with an average answer length of 150 words. We have minimized textual redundancy in the questions, eliminating unnecessary contextual information, distracting conditions, and attributes readily observable from the diagrams. This reduction in text forces MLLMs to enhance their capability to extract essential content from visual inputs. MAVISInstruct is assembled from four distinct sources to ensure broad coverage. Manual Collection Augmented by GPT-4. To incorporate high-quality problems found in realworld contexts, we manually collect 4K math problems with diagrams from publicly available resources. Recognizing that these sources often lack detailed rationales and may contain redundant text, we initially utilize GPT-4V to annotate a detailed solving process and streamline the question text to reduce redundancy. Subsequently, for each collected instance, we input the question, rationale, and diagram into GPT-4 and employ customized few-shot prompts to generate 20 new problems per original, comprising 15 multiple-choice questions and 5 free-form questions. This process contributes a total of 84K problems to the dataset. Existing Datasets Augmented by GPT-4. Given existing well-organized geometric datasets, we can also leverage them to expand MAVIS-Instruct. Referring to previous prompt designs, we augment the 8K training set from two dataset, Geometry-3K and GeoQA+, into 80K visual problems with accompanying rationales, mapping each original problem to 10 new ones. Due to the scarcity of publicly available function data, we do not include function problems from this source. Data Engine Captions Annotated by GPT-4. Given the detailed captions and diagrams generated by our data engine, we can prompt GPT-4V with these sufficient conditions to generate accurate question-answering data. We first generate a new set of 17K diagram-caption pairs that do not overlap with the previous MAVIS-Caption, which avoids answer leakage within the detailed caption. Then, we prompt GPT-4V to generate 3 new problems with rationales, obtaining 51K data in total from the diagram-caption pairs. Data Engine Generated Problems. In addition to relying on GPT for data generation, we manually craft rigorous regulations to produce visual math problems directly from our data engine. • Plane Geometry Problems. We initially prompt GPT-4 to compile a comprehensive set of mathematical formulas applicable to each basic shape (e.g., Pythagorean theorem for right triangles and area formula for circles). Then, for a geometric diagram, we randomly select a known condition within a shape as the final solution target, and systematically deduce backward to another condition, either within the same shape or an adjacent one, using a randomly selected mathematical formula. This deduced condition is then set as unknown, and we continue iterative backward deductions as necessary. The final condition, along with any conditions in the last step, are presented as initial attributes in the question. The rationales can be simply obtained by reversing this backward deduction process. • Function Problems. As the properties of functions are predetermined, we utilize GPT-4 to generate diverse reasoning templates. These templates facilitate the solving of one function property based on other provided properties, thereby ensuring the generation of high-quality function rationales. We finally obtain 299K plane geometry and 212K function problems. 4 Mathematical Visual Training With the curated datasets, we devise a three-stage training pipeline for endowing MLLMs with mathematical visual capabilities. They respectively aim to mitigate the three deficiencies within existing MLLMs, i.e., diagram visual encoding, diagram-language alignment, and mathematical reasoning skills in visual contexts. 4.1 Stage 1: Training CLIP-Math To enhance CLIP’s [51] inadequate visual encoding of math diagrams, we utilize MAVIS-Caption to train a specialized CLIP-Math encoder. Specifically, we fine-tune a pre-trained CLIP-Base model following the conservative learning scheme. The math diagrams are fed into the learnable vision encoder, while the corresponding captions are processed by the text encoder, which remains frozen to provide reliable supervision. Via contrastive training, the model learns to adapt from its original natural image domain to mathematical contexts, increasing its focus on essential visual elements within diagrams, as demonstrated in Figure 1 (a). The optimized CLIP-Math encoder now delivers more precise and robust representations of math diagrams, establishing a solid foundation for the subsequent visual interpretation of LLMs. 4.2 Stage 2: Aligning Diagram-language After acquiring the CLIP-Math encoder, we further integrate it with LLMs using MAVIS-Caption to boost cross-modal alignment between math diagrams and language embedding space. Using a simple two-layer MLP as the projection layer, we transform the visual encodings from CLIP-Math, and prepend them as a prefix to the LLM input. This process, guided by the diagram captioning task, enables the LLM to accurately recognize mathematical components and describe their spatial arrangements. With the diagram-language alignment, LLMs are equipped with the interpretation capability in math diagrams, serving as an initial step toward deeper mathematical reasoning. In this stage, we freeze the CLIP-Math, and train the projection layer along with the LoRA-based [27] LLM. 4.3 Stage 3: Instruction Tuning Lastly, we leverage MAVIS-Instruct to endow MLLMs with CoT reasoning and problem-solving capabilities in visual mathematics. The detailed rationales within each problem’s solution provide high-quality reasoning guidance for MLLMs, significantly enhancing their step-by-step CoT process. Furthermore, the adopted text-lite, vision-dominant, and vision-only problem formats facilitate MLLMs to capture more essential information from the visual embeddings for problem-solving, rather than relying on shortcuts to only process the textual content within questions. During this stage, we unfreeze both the projection layer and the LoRA [27]-based LLM to perform a thorough instruction-following tuning, which finally results in MAVIS-7B.